En utvidet lineær regresjonsmodell
Vi starter gjerne en analyse av områdedata med å lage et tematisk kart av utfallsvariabelen, for eksempel forekomsten av sykdom. Figur 1a viser et slikt kart for insidensrate av covid-19 for de første 250 dagene av pandemien i Oslo (2). Vi ser at bydelene Alna og Vestre Aker skiller seg ut som bydelene med høyest og lavest smitte.
Under pandemien var det viktig å få kunnskap om hvordan sosioøkonomiske forhold i de ulike bydelene var knyttet til forekomsten av sykdom (3). Figur 1b viser et kart over gjennomsnittsinntekten for husholdningene i Oslos bydeler. Her ser vi at bydelene Nordre Aker og Alna ligger henholdsvis øverst og nederst på inntektslisten (4).
Det finnes flere modeller for hvordan man kan undersøke slike potensielle sammenhenger, f.eks. modellen som heter spatial lag model (5). Det er en utvidelse av en lineær regresjonsmodell. Vi kjenner igjen termene fra en regresjonsmodell, men vi inkluderer et ekstra ledd på høyre side av likningen: 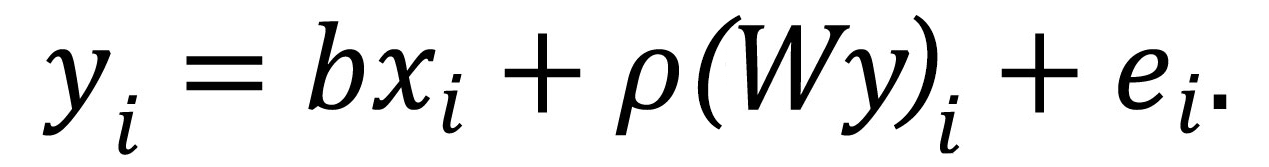
Her er utfallsvariabelen vår yi, mens forklaringsvariabelen er xi. Parameteren b er regresjonsparameteren vi er interessert i, og den beskriver sammenhengen mellom utfalls- og forklaringsvariablene, mens W er en matrise som holder orden på naboskapet til de ulike bydelene. Matrisen vil ha en positiv verdi for de bydelene som er naboer, og er ellers 0. Parameteren ρ sier noe om styrken i den romlige avhengigheten. Til slutt har vi et feilledd: ei.
Det som skiller denne modellen fra en lineær regresjonsmodell, er leddet Wyi. Dette leddet inneholder opplysninger om utfallsvariabelen fra naboområdene, og det er derfor den har fått navnet «lag». Når vi inkluderer dette leddet, tar vi hensyn til den romlige avhengigheten mellom områdene.
Vi tilpasser nå modellen over med verdiene vist i figur 1, og her ble regresjonsparameteren b lik -3,92 (95 % konfidensintervall -6,11–-1,72). Når gjennomsnittsinntekten økte med 1 000 kroner, ble forventet insidensrate redusert med 3,92 personer per 100 000. Vi tilpasser også en ordinær lineær regresjonsmodell, og her ble resultatet -3,80 (-6,01–-1,54). Regresjonsparametrene i dette eksempelet ble relativt like, og den romlige avhengigheten er derfor også liten. I andre tilfeller kan romlig avhengighet ha større betydning.
Modellen som er vist her, kan tilpasses i programmer som R og Stata. Selv om modellene er mer krevende enn en lineær regresjonsmodell, vil de gi mer presise resultater fordi de tar bedre hensyn til hvordan data genereres.