Being able to estimate the expected number of non-elective births on a given day, and thus how the activity in maternity wards will vary through the week and the year, is a considerable advantage for heads of maternity clinics and other decision-makers in the health services. This will assist in planning for an optimal staffing and resource strategy at the local maternity ward, as well as in understanding how the size of the maternity ward is related to the expected variations. A maternity ward has a low proportion of elective procedures combined with relatively acute needs among its patients, and the quality of the services may therefore be vulnerable to major fluctuations in the inflow of patients. Having a good model of the distribution of births is an advantage for predicting birth-frequency peaks and quantifying the residual uncertainty to permit accumulation of an adequate reserve capacity.
Many studies of the distribution of births have been published, seasonal variations have been well described, and many find an excess frequency of births on Mondays and a relative paucity during weekends and public holidays (1) – (10). Most of these studies are old, however, and have not been corrected for elective births, i.e. elective Caesarean sections and induced births. Since elective births to some extent are planned, inclusion of these will disrupt the natural variation in birth rates. Moreover, they represent less of a problem for planning of perinatal care, since they can be moved to another and more convenient time. As far as we are aware, there is only one recent Danish study that has excluded elective births (9). The study found that births follow the Poisson distribution (11), with seasonal variations and – somewhat unexpectedly – that a considerable variation in terms of days of the week still prevails, with fewer births occurring during weekends. An article in a non-peer-reviewed journal (12) referred to in the Journal of the Norwegian Medical Association (13) claimed that the digit sum of the date number (Box 1) is an explanatory variable for the expected number of births on a given day. More specifically, the hypothesis says that the lower the digit sum, the higher the expected number of births (12, 13). Furthermore, it is claimed that the digit sum of the birth dates (defined as the sum of the digits comprising the date on which the birth took place) follow the so-called Benford distribution (14).
Digit sum
The date number of a day is simply the ordinal number of the date: for example, Friday 13 March has the date number 13. The digit sum of a number written in the common decimal system is found by adding up the digits in the number. Next, we repeat this operation until we are left with a number between 1 and 9. For example, the digit sum of 21 equals 2+1=3, while the digit sum of 29 is 2+9=11 and subsequently 1+1, so that the digit sum of 29 equals 2.
In our study we have tested these results with the aid of data on non-elective births from Akershus University Hospital in Lørenskog municipality. Our objective was to examine the following hypotheses:
Births follow the Poisson distribution with systematic variations across weeks and months.
Births follow the Benford distribution across date numbers, and there is a cluster of births on dates for which the digit sum is low.
Material and method
Theory
The timing of a birth is based on the time of conception and the length of the gestation. We assume that a good model for the number of conceptions is presented by a (time-dependent) Poisson process, since the conceptions are independent events. In mathematical terms, this means that the expected waiting time until the next conception is negatively exponentially distributed:
Expected waiting time until the next conception is λ–1 (β)
with the variance λ–2 (β),
where β = β₁, …, βk are parameters that may vary over time, for example with the seasons. The resulting Poisson process has an expected number of conceptions per time unit equal to λ(β) with the same variance λ(β). If the above is an appropriate approach to the conception process at the population level, it follows that births are also an approximate Poisson process, with some extra variance attributable to the variable length of gestation periods. Since parameters may vary over time, an underlying Poisson distribution of births does not exclude some systematic variation attributable to factors in the period around the delivery, including explanatory variables associated with days of the week or date numbers. In addition, the tendency towards more frequent elective deliveries may have an effect on the quality of this model; for example, the proportion of Caesarean sections in Norway has increased from 1.8 % in 1967 to 16.9 % in 2013 (15).
Data
The data material in this study includes the dates of all births at Akershus University Hospital in the period 1 January 1999 – 31 December 2014 (N = 65 528). As a participant in an internal analysis project at the maternity ward, the first author had access to these data, the use of which has been approved by the hospital’s data protection officer. The data consisted of a single table, which listed the number of spontaneous births for each date in the period in question. Multiple births are counted as a single birth per child. In a large data set, elective births may for example lead to a lower frequency of births on the first day of the month in Norway. This is because over the year, we have two fixed holidays on the first day of a month (1 January and 1 May), on which fewer births are induced and fewer Caesarean sections are planned.
Some births start spontaneously, but end with an acute Caesarean section. These births have been counted in the data used for the main analyses. All analyses have also been repeated on a reduced data set, in which spontaneous births ending in Caesarean sections were excluded in the birth count for each date.
The data used in the analyses were anonymised and do not contain any personally identifiable information.
Analyses
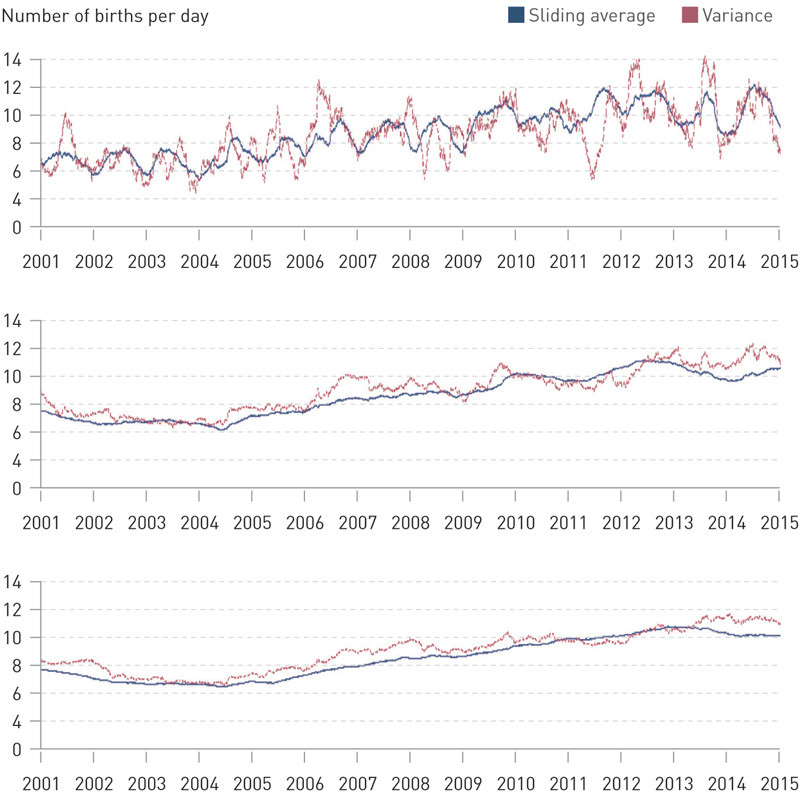
All statistical analyses were performed in the statistics tool R (16, 17). We plotted a sliding average (over 90, 360 and 720 preceding days, respectively) for the number of non-elective births against the variance for the same period, for the period 1 January 2001 – 31 December 2014.
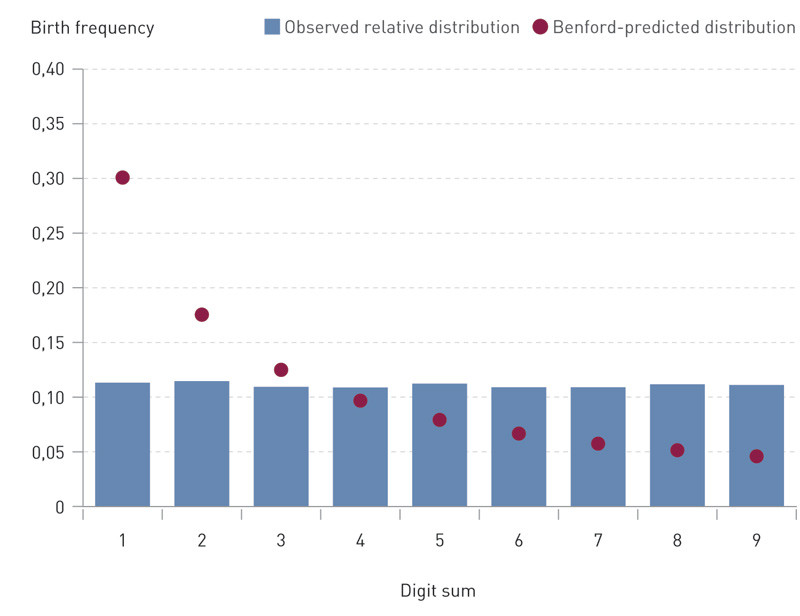
We also plotted the relative frequencies of the sums of the digits of the birth dates against the Benford distribution and performed a chi-square (χ²) goodness-of-fit test (17) on the observed frequencies. In such a test, the null hypothesis says that the data follow the Benford distribution, meaning a higher likelihood of rejection of the null hypothesis the lower the p-values observed. The frequencies of the sums of the digits in the birth dates were calculated for birth date numbers ranging from 1 to 27. The reason is that otherwise we would see a clustering on 1 – 4, since these sums occur with a higher frequency than the remaining dates (the dates 28, 29, 30 and 31 account for one extra day with the sums 1 – 4 in the months where they occur).
We specified various Poisson regression models, all having NoB (number of births on a given day) as their outcome variable. In a Poisson regression model, we assume that the outcome variable follows the Poisson distribution, as opposed to a regular regression model, which is based on a normal distribution. The Poisson distribution is the most commonly used distribution to model variables defined over non-negative integers, which typically characterise situations where the number of events are counted over a specified time. The explanatory variables included various combinations of years, months and days of the week (UKD) (1999, January and Sunday are reference categories for these explanatory variables), as well as the sums of the digits (TVS) of the date number (1) – 31). We assessed the merits of each of the models with the aid of standard model selection methods: the Akaike information criterion, AIC) ((18), the determination coefficient R² (19) and the likelihood ratio.
Any significant variation in terms of days of the week or sums of date digits revealed by the regression analysis was described as the expected percentage increase on the days of the week/date numbers in question.
Results
Altogether 50 017 births initiated spontaneously were analysed. Of these, the 46 748 that did not end in an acute Caesarean section were included in a separate, additional analysis. The figures presented below are based on the 50 017 former. In both cases, the figures are near-identical. This means that none of the variables in our analysis – day of the week, season, year or digit sum – have an effect on the likelihood that a spontaneously initiated delivery will end in an acute Caesarean section.
Plots of sliding averages
The curves for sliding averages and variances over the last 90, 360 and 720 days respectively are presented in Figure 1. In the figure for the 90-day average we can see a clear seasonal variation. For a Poisson process we expect the variance to follow the average. The result in Figure 1 appears to be consistent with an underlying Poisson process: the variance does not deviate that much from the average, it varies around the average, and the variance is more equal to the average when estimated for longer periods. Furthermore, we can see that the average number of non-elective births per day increases from 2005 before receding from mid-2012 and rebounding towards the end of 2014.
Distribution of the digit sums
A plot of the distribution of the digit sums for the 44 470 births with date numbers 1 – 27 is shown against a Benford distribution in Figure 2, demonstrating a major deviation. The Benford goodness-of-fit test (p = 0.007425) disproves the hypothesis that the digit sums of the dates of birth follow the Benford distribution.
Regression analysis – choice of model
The regression analyses show that year and month were important explanatory variables. Table 1 shows the selection criteria for models that included the two remaining explanatory variables, day of the week UKD and digit sum TVS, that potentially may describe other time dependencies.
Table 1
Model selection criteria for models that include the two remaining explanatory variables day of the week and digit sum, that potentially may describe other time dependencies. We assessed the merits of the models with the aid of standard model selection methods: the Akaike information criterion (AIC), the determination coefficient R² and the likelihood ratio test
| Model |
AIC |
R² |
P-value¹ |
(Comparator)¹ |
| Basic model (G)² |
29017.0 |
0.225 |
– |
– |
| G + Day of the week |
29002.5 |
0.229 |
< 0.001 |
(G) |
| G + Digit sum |
29017.5 |
0.225 |
= 0.229 |
(G) |
| G + Day of the week + Digit sum |
29003.1 |
0.229 |
= 0.231 < 0.001 |
(G+UKD) (G+TVS) |
| [i] | ||||
[i] ¹ The p-value for the likelihood ratio test with a comparator model shown in brackets to the right of the p-value. A low p-value means a significantly improved goodness-of-fit
² Model with explanatory variables for year and month
All Poisson regression models that did not include both year and month fitted the observations poorly. This was indicated by the likelihood ratio test against a model with no explanatory variables (p < 0.001) and the Akaike information criterion (not shown). The opposite held for all models that included year and month (goodness-of-fit test, p > 0.100). The AIC score was lower in models that included the digit sum as a variable and the day-of-the-week variable than in the models from which these were excluded. The determination coefficient R² indicates that including the digit sum as a variable does not increase the model’s explanatory power, but the day-of-the-week variable does. Stepwise chi-square testing of models that included the day of the week and the digit sum as variables shows that the model with the day-of the-week variable fits the model significantly better than the model that included the sum-of-the-digits variable, and that the latter variable contributes no predictive value. A likelihood ratio test of whether the model is improved by including the digit sum in addition to the day of the week gave a non-significant result.
The model that stood out as the best included the explanatory variables year, month and day of the week.
Regression analysis – the best model
The annual variation has already been described above. The monthly variation shows a peak in the summer months and a trough from October to January. Variation by day of the week was marked, with pronounced peaks on Fridays and Tuesdays in contrast to a lower expected number of spontaneous births on Wednesdays and Thursdays and an even lower expected number of births on Saturdays and Sundays (Table 2).
Table 2
Expected number of excess births on weekdays relative to Sundays, as a percentage. Inclusion of day of the week as a variable gave a significantly better goodness-of-fit (p
| Day of the week |
Regression coefficient |
Relative to Sunday (%) |
| Monday¹ |
0.0568 |
5.8 |
| Tuesday¹ |
0.0725 |
7.5 |
| Wednesday² |
0.0336 |
3.4 |
| Thursday³ |
0.0525 |
5.4 |
| Friday¹ |
0.684 |
7.1 |
| Saturday |
0.3525 |
3.6 |
| Sunday |
Ref. |
0.0 |
| [i] | ||
[i] ¹ (p < 0.001)
² (p < 0.05)
³ (p < 0.01)
All the analyses that excluded births ending in an acute Caesarean section showed the same results, with near-identical coefficients, goodness-of-fit parameters and p-values.
Discussion
This study shows that spontaneously initiated births are well modelled by a time-dependent Poisson process when variations by month and day of the week are included. The variations by month and day of the week have a high predictive value: the frequency of births is highest in the months of June and July, and Fridays and Tuesdays stand out as the busiest days of the week. The birth frequency is at its lowest during weekends. Furthermore, we found that the sums of the digits of date numbers do not follow the Benford distribution. There is no clustering of births on days with a low sum of their digits. The digit sum has no explanatory force and can be omitted from models of birth frequency.
One possible source of error in this context is the practice followed in periods with a high number of expected births of sending women to other nearby hospitals with expected free capacity. This may lead to observation of a lower variance than would be predicted by a Poisson model, since there will be fewer days with a very high number of births than the model would indicate.
There is no reason to reject the hypothesis that a Poisson process constitutes an appropriate mathematical model for the expected number of non-elective births. The hypothesis put forward that the digit sum of the date number has an effect on birth rates (12, 13), with a Benford distribution or otherwise, can be rejected. The goodness-of-fit tests with a view to a Poisson distribution lends strong support to the results of Gam and collaborators (9), and our findings confirm the general pattern of seasonal variability described by Aarnes and Andersen (10).
This may have implications for decision-makers in the health services. With regard to the activity planning in maternity wards, some economies of scale may be reaped with a view to the variations in the number of births from one day to the next. If we assume that the arrival of new mothers-to-be follows the Poisson distribution, the standard deviation will increase by the square root of the expected number of births. This means that if some excess capacity is included in planning in order to cope with the peaks, these will be relatively lower in one large ward than in two smaller ones. For example, a ward with an expected number of eight births daily would presume that the number of daily births will exceed fifteen on only one per cent of all days. Similarly, a ward with ten expected births daily may anticipate that the number of births will exceed eighteen on only one per cent of the days. In a large ward with eighteen births expected daily, this figure will amount to 29. In other words, the two smaller wards will need to plan for a total capacity of 33 births, four more than the large one. For a general discussion of the advantages of larger units in terms of predictability of arrivals when these constitute a Poisson process, see Kirkwood and Sterne (11, p. 234). Another possibility could be to schedule some elective births to Wednesdays and Thursdays, or make provisions for elective «weekend sections».
The fact that birth rates vary with the seasons is well known and well understood. Like those of Aarnes and Andersen (10), our findings show that the September peak described by Ødegård (1) has moved to earlier in the year. One possible explanation for this shift could be that the admission to day-care in any one year requires the child to have been born before 1 September of the previous year.
The finding of a strong and significant variation by day of the week for births confirms the somewhat unexpected finding of such a variation in the Danish study (9). Why does it seem that even non-elective births «get done with» on Fridays and/or are delayed until Monday or Tuesday? One possible explanation could be that pregnant women have different ways of living on weekends and weekdays, with a differing effect on the start of labour. Other possible explanations could be that perinatal care practices may differ slightly on weekends as opposed to weekdays, or that pregnant women are more often referred to other hospitals on weekends than on weekdays.
Beyond lending support to the hypothesis that births follow the Poisson distribution, the analyses of birth data from Akershus University Hospital should not be over-interpreted. We have only analysed the number of non-elective births, and we have not controlled for other variables.
To sum up, we found that births follow a (time trend-adjusted) Poisson distribution, with variations by month and day of the week, and that the date number has no explanatory force.
MAIN MESSAGE
Spontaneously initiated births are well modelled by a time-dependent Poisson process when variations by month and day of the week are included.
The highest birth frequencies are in June and July, and Fridays and Tuesdays stand out as the busiest days.
Birth frequencies are at their lowest during weekends.
- 4.
Brunborg H. Få fødsler, mange unnfangelser. www.ssb.no/befolkning/artikler-og-publikasjoner/fa-fodsler-mange-unnfangelser (5.10.2015).
- 11.
Kirkwood BR, Sterne JAC. Essential medical statistics. 2. utg. Malden, MA: Blackwell Science, 2003: 501.
- 12.
Dønvold T. Sesongjusterte fødselsdata er ikke uniformt fordelt. Tilfeldig Gang 2014; nr. 2: 5. https://sites.google.com/site/statistiskforening/tilfeldig-gang (23.10.2015).
- 13.
Dønvold T. Sesongjusterte fødsler er ikke jevnt fordelt på datoer. Tidsskr Nor Legeforen 2014; 134: 1834.
- 14.
Wikipedia. Benford’s law. https://en.wikipedia.org/w/index.php?title=Benford%27s_law&oldid=682325873 (5.10.2015).
- 15.
Medisinsk fødselsregister. http://mfr-nesstar.uib.no/mfr/ (10.5.2015).
- 16.
The R Foundation. The R project for statistical computing. www.R-project.org/ (5.10.2015).
- 17.
Joenssen DW. BenfordTests: Statistical tests for evaluating conformity to Benford’s law. http://CRAN.R-project.org/package=BenfordTests (10.5.2015).
- 18.
Akaike H. Information theory and an extension of the maximum likelyhood pinciple. I: Selected Papers of Hirotugu Akaike. Berlin: Springer Science & Business Media, 1998: 199 – 213.
- 19.
Colin Cameron A, Windmeijer FAG. An R-squared measure of goodness of fit for some common nonlinear regression models. J Econom 1997; 77: 329 – 42. [CrossRef]